📍 Statistical object recognition, PCA/LDA, SVD
2024년 연세대학교 컴퓨터과학과 4학년 과목인 Computer Vision을 수강하며...
#1. Object recognition에서 categorization에 대한 statistical한 관점
베이즈 정리 (Bayes Rule) 이용: p(zebra | image) = p(image | zebra) p(zebra)
- 사후 확률 (Posterior): p(zebra ∣ image)
- 우도 (Likelihood): p(image ∣ zebra)
- 사전 확률 (Prior): p(zebra)
MAP decision (Maximum a Posteriori Decision):
결국 우리의 목적은 posterior가 최대가 되도록 하는 결정 기준을 세우는 것. 즉, 이미지가 주어졌을 때 그 이미지가 특정 category에 속할 확률이 최대가 되게 하는 결정 기준을 세우는 것이다.
이는 두 가지 방식으로 달성할 수 있다.
Discriminative methods: model posterior (p(zebra ∣ image))
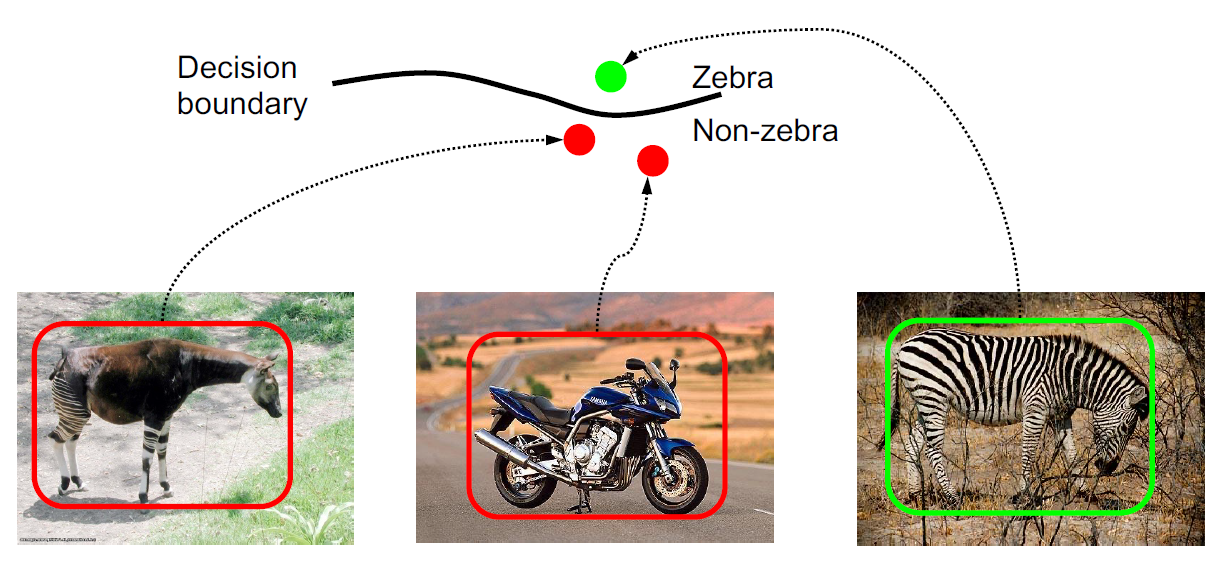
Generative methods: model likelihood and prior (p(image ∣ zebra), p(zebra))
p(image | zebra), p(image | no zebra)에 대해 이미지마다 아래와 같이 평가할 수 있음

middle->low는 이미지가 zebra가 아닌 경우 해당 이미지일 확률에 대해 모델이 초기에는 중간 확률(Middle)을 할당할 수 있지만, 추가적인 정보나 학습 과정을 통해 그 확률이 낮아질(Low) 수 있음을 나타내는 것이다.
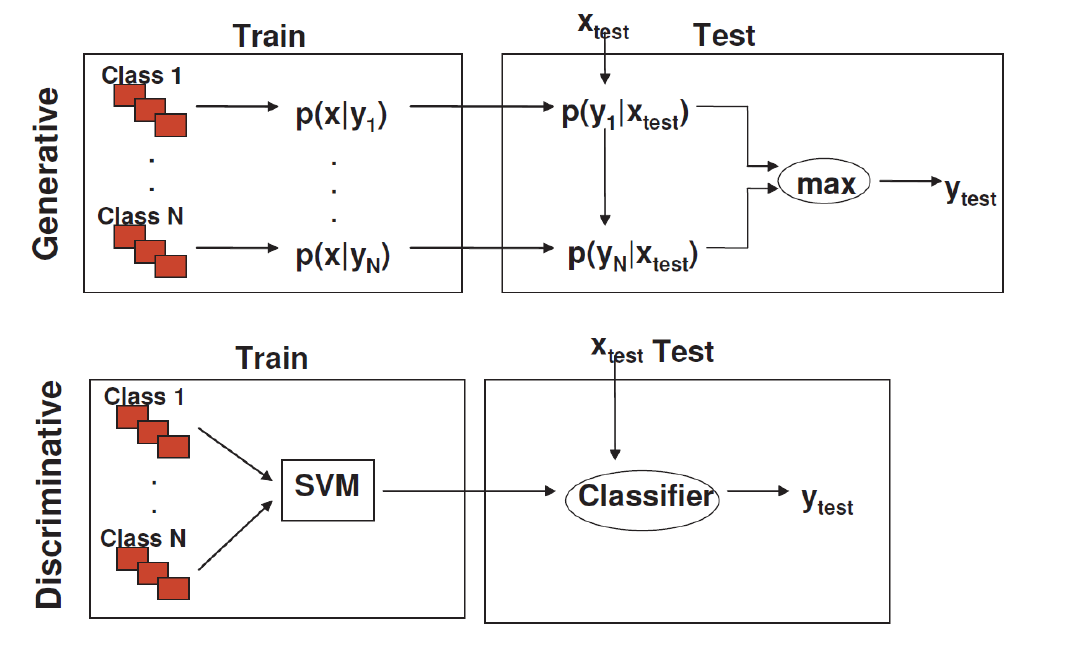
결국 두 방식을 비교하면 다음과 같다.
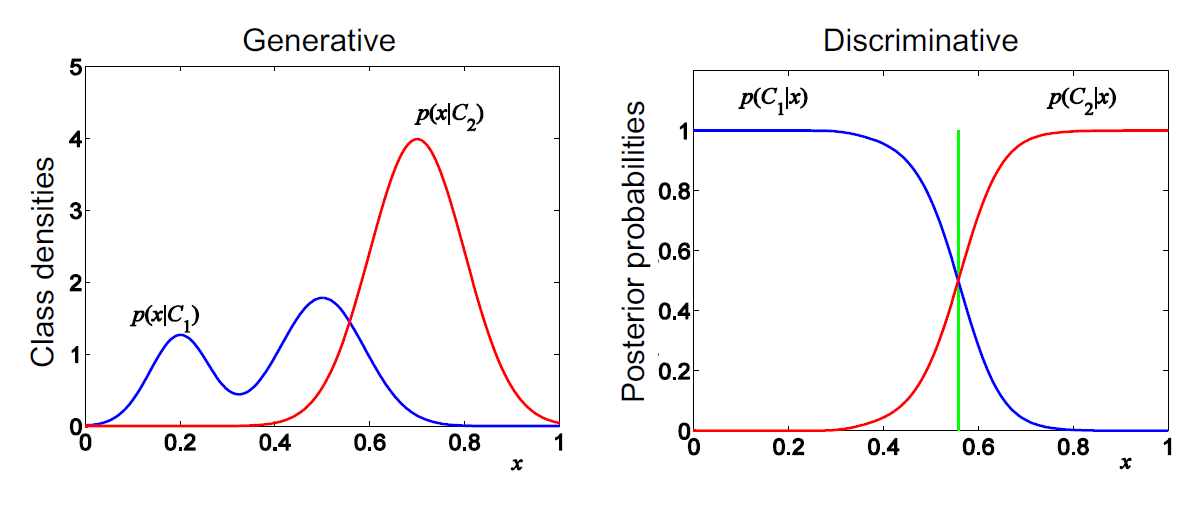
C는 class를 나타낸다. generative method는 각 class 내에서 특정 값 x가 발생할 확률을 표현할 수 있고, discriminative method는 특정 값 x가 있을 때 class1일 확률, class2일 확률을 표현할 수 있다.
=> 결국 generative model은 클래스 간의 분포를 명확히 모델링할 수 있고 category가 하나만 있어도 모델링이 되지만, 복잡한 분포를 다루기 어려울 수 있다. 그리고 decision에 있어서 애초에 likelihood를 모델링할 필요가 없는 경우도 있다. 반면 discriminative model은 직접적으로 분류 문제를 해결해(이미지가 있을 때 class 맞히기) 효율적이고 classification rate가 보통 더 좋은데, 클래스 간의 분포를 이해하는 데는 제한적일 수 있다.
#2. Bag-of-Words Image Representation
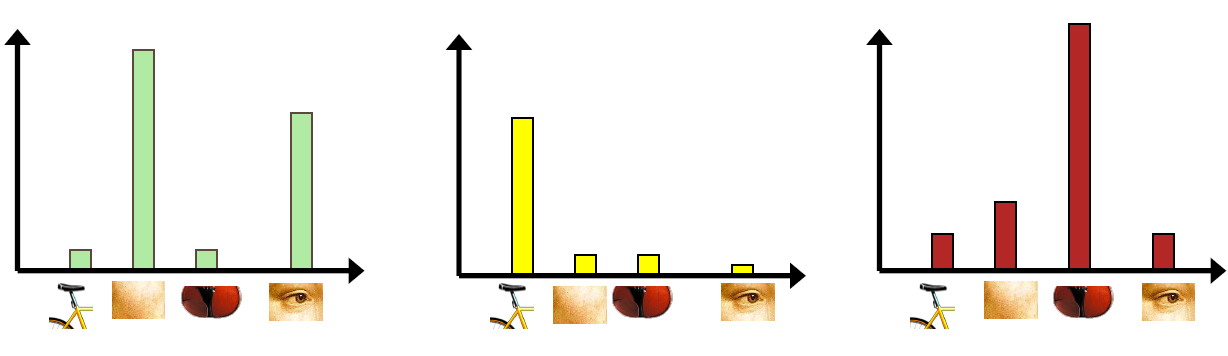
- 기원 1: 텍스처 인식 (Texture Recognition):
- 텍스처는 basic element나 texton의 반복으로 특징지어짐.
- 텍스처 인식에 중요한 것은 texton의 identity이지 이것의 공간적 배열이 아님. -> 히스토그램
- 기원 2: Bag-of-Words 모델:
- 단어의 빈도수를 기반으로 한 문서의 순서없는 표현. -> 이것도 결국 히스토그램
- 결국.. "이미지 분류를 위한 Bag-of-Features"이란
- 특징 추출 -> visual vocabulary 학습 -> feature를 visual vocabulary로 quantization -> 히스토그램
- visual vocabulary 학습에서 clustering을 씀: K-means clustering
- cluster center m(ramdomly initialization)에 대해 요소 x와 m의 거리를 다 더해 sum of squared Euclidean
distances(D)를 계산하여 D를 minimize하기 위한 학습 진행 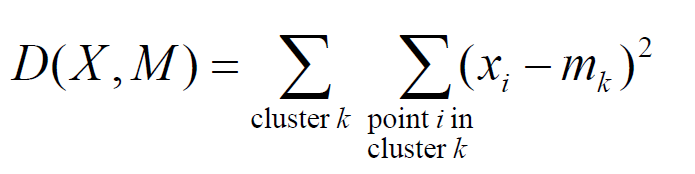
- 특징 추출 -> visual vocabulary 학습 -> feature를 visual vocabulary로 quantization -> 히스토그램
PCA (PRINCIPAL COMPONENT ANALYSIS), 주성분 분석
언제 쓰냐? high dimension data 분석할 때, algorithm 복잡도 낮출 때, denoising할 때, 정보 compress할 때
(잠깐! remind. PCA vs. LDA)

PCA Step:
• Mean center the data
• Compute covariance matrix Sigma
• Calculate eigenvalues and eigenvectors of Sigma
• Eigenvector with largest eigenvalue_1 is 1st principalcomponent (PC)
• Eigenvector with kth largest eigenvalue_k is kth PC
• eigenvalue_k / eigen 총합 = proportion of variance captured by kth PC

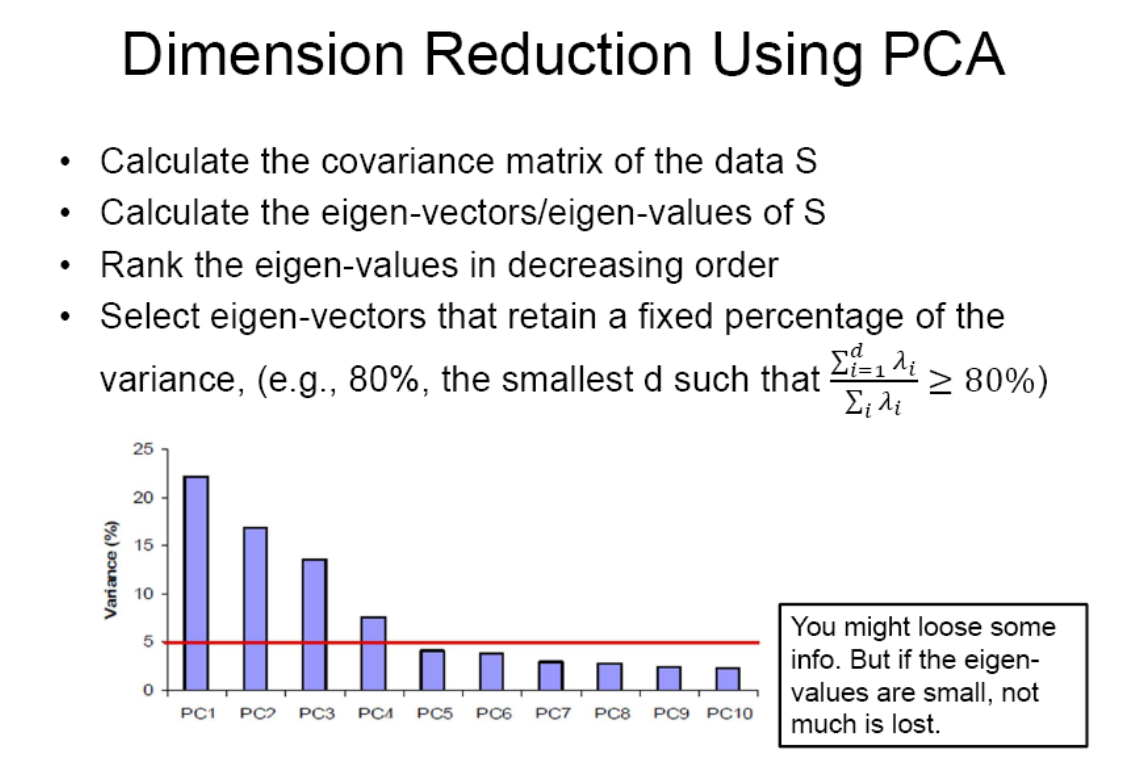

PCA로 data를 preprocessing하면 좋은 점:
* Reduced dimension -> simpler hypothesis space
* Reduced noise
PCA 사용시 주의점:
* Fails when data consists of multiple separate clusters. (이것도 LDA 쓰는 게 좋을 때를 뜻함.)
* Directions of greatest variance may not be most informative (PCA가 분산이 가장 큰 방향을 주성분으로 하는 것인데 이 자체가 최선이 아닐 수 있음). 예를 들어 class 구분할 때는 PCA 대신 LDA 쓰는 게 좋음.
* 속도 느릴 수 있음
-> 계산을 단순화, 효율화하여 빠르고 안정적으로 PCA 연산을 하기 위해 SVD algorithm을 쓰자!


여기서 는 X*X^T의 고유벡터로 구성된 직교 행렬, 는 대각 행렬, V는 직교 행렬인데, U를 PCA의 W로 쓰면 된다.
'Study > Computer Vision' 카테고리의 다른 글
| [CV] ViT, ViViT (Vision Transformer, Video Vision Transformer) (0) | 2024.07.05 |
|---|
